|
template<matrix_order RO, matrix_style RS, typename T , matrix_order PO1, matrix_style PS1, matrix_order PO2, matrix_style PS2, matrix_order PO3, matrix_style PS3>
Fast caclulation of This function calculates Matrices conform when A, B, and C are chosen with dimensions Scythe will use LAPACK/BLAS routines to compute
References scythe::Matrix_base< ORDER, STYLE >::cols(), scythe::Matrix_base< ORDER, STYLE >::isScalar(), scythe::Matrix_base< ORDER, STYLE >::rows(), and SCYTHE_THROW. |
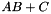 .
.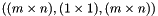 ,
, 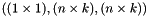 , or
, or 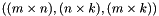 .
.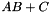 with column-major matrices of double-precision floating point numbers if LAPACK/BLAS is available and you compile your program with the SCYTHE_LAPACK flag enabled.
with column-major matrices of double-precision floating point numbers if LAPACK/BLAS is available and you compile your program with the SCYTHE_LAPACK flag enabled.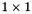 or
or 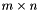
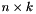
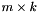
 1.7.6.1
1.7.6.1