|
|
template<matrix_order RO, matrix_style RS, typename T , matrix_order PO1, matrix_style PS1, matrix_order PO2, matrix_style PS2, matrix_order PO3, matrix_style PS3>
| Matrix<T,RO,RS> scythe::chol_solve |
( |
const Matrix< T, PO1, PS1 > & |
A, |
|
|
const Matrix< T, PO2, PS2 > & |
b, |
|
|
const Matrix< T, PO3, PS3 > & |
M |
|
) |
| |
Solve 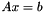 for x via backward substitution, given a lower triangular matrix resulting from Cholesky decomposition. for x via backward substitution, given a lower triangular matrix resulting from Cholesky decomposition.
This function solves the system of equations 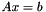 via backward substitution. L is the lower triangular matrix generated by Cholesky decomposition such that via backward substitution. L is the lower triangular matrix generated by Cholesky decomposition such that 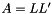 . .
This function is intended for repeatedly solving systems of equations based on A. That is A stays constant while b varies.
- Parameters:
-
| A | A symmetric positive definite Matrix. |
| b | A column vector with as many rows as A. |
| M | The lower triangular matrix from the Cholesky decomposition of A. |
- See also:
- chol_solve(const Matrix<T,PO1,PS1>&, const Matrix<T,PO2,PS2>&)
-
cholesky(const Matrix<T, PO, PS>&)
-
lu_solve (const Matrix<T,PO1,PS1>&, const Matrix<T,PO2,PS2>&, const Matrix<T,PO3,PS3>&, const Matrix<T,PO4,PS4>&, const Matrix<unsigned int, PO5, PS5>&)
-
lu_solve (Matrix<T,PO1,PS1>, const Matrix<T,PO2,PS2>&)
- Exceptions:
-
References scythe::Matrix_base< ORDER, STYLE >::isColVector(), scythe::Matrix_base< ORDER, STYLE >::isNull(), scythe::Matrix_base< ORDER, STYLE >::isSquare(), scythe::Matrix_base< ORDER, STYLE >::rows(), and SCYTHE_CHECK_10.
|
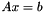 for x via backward substitution, given a lower triangular matrix resulting from Cholesky decomposition.
for x via backward substitution, given a lower triangular matrix resulting from Cholesky decomposition. 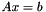 via backward substitution. L is the lower triangular matrix generated by Cholesky decomposition such that
via backward substitution. L is the lower triangular matrix generated by Cholesky decomposition such that 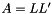 .
. 1.7.6.1
1.7.6.1